
Vector D = m_xDisplacement - xBody.m_xDisplacement ĭ = -(1.
Vector 2d collision code#
Here are two diagrams of what I'm talking about.Ĭan anyone point me into a right direction please?Īll information that can be given after the collision is the minimum penetration vector.ĮDIT: Found some code online that's very related to this but I don't understand it: void CBody::ProcessCollision(CBody& xBody, const Vector& N, float t) IntervalDistance = Math.Currently I have a mini physics game which uses Separating Axis Theorem for collision detecting and response, however I came to a standstill when I discovered that there wasn't much documentation on what happens to an object's velocity after it collides with another shape using SAT collision detection. This will be used to calculate the minimum translation vector If so store // the interval distance and the current distance. Check if the current interval distance is the minimum one. If the polygons are not intersecting and won't intersect, exit the loop if (!result.Intersect & !result.WillIntersect) break Get the projection of polygon A during the movement if (velocityProjection 0) result.WillIntersect = false

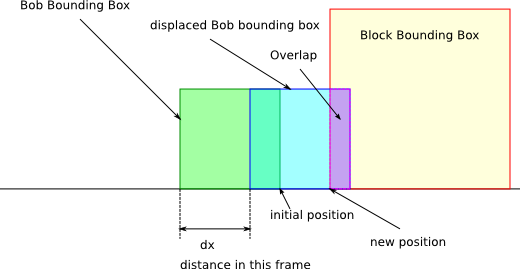
Now find if the polygons *will* intersect = // Project the velocity on the current axis float velocityProjection = axis.DotProduct(velocity) Loop through all the edges of both polygons for ( int edgeIndex = 0 edgeIndex 0)\ PolygonCollisionResult result = new PolygonCollisionResult() įloat minIntervalDistance = float.PositiveInfinity velocityA - velocityB) public PolygonCollisionResult PolygonCollision(Polygon polygonA, The last parameter is the *relative* velocity // of the polygons (i.e. The PolygonCollision() function does all of the above, and returns a PolygonCollisionResult structure containing all the necessary information to handle the collision:Ĭopy Code // Check if polygon A is going to collide with polygon B. That is it! Now, each time a collision occurs, the first polygon will nicely slide along the surface of the other polygon.įigure 1: Projections of the polygons onto an axis.įigure 2: Projections for moving polygons.įigure 3: Find the minimum interval overlapping, then calculate the translation required to push the polygons apart. Then, the amount of translation will simply be the amount of overlapping on this axis (Fig. We will push the first polygon along this axis. The axis on which the projection overlapping is minimum will be the one on which the collision will take place. Once we have found that the polygons are going to collide, we calculate the translation needed to push the polygons apart.

We need to do the test for all the edges before knowing that.) (NB: However, remember that if the intervals do overlap, it doesn't necessarily mean that the polygons will collide. From there, you can use the technique used for static polygons: if the projections of polygons A and B don't overlap, the polygons won't collide. This will give you the interval spanned by the polygon over the duration of the motion. Extend the projection of the first polygon by adding to it the velocity projection (Fig. After having checked that the current projections do not overlap, project the relative velocity of the polygons on the axis. This can be easily extended to deal with moving polygons by adding one additional step. If these projections don't overlap, the polygons don't intersect (exit the loop).Find the axis perpendicular to the current edge.The implementation of this theorem is relatively simple, and could be summed up in this pseudo code: The idea is to find a line that separates both polygons - if such a line exists, the polygons are not intersecting (Fig. collisions only - no gravity, rigid body handling, or complex solvers. consistent vector/matrix/line representation. None satisifed all of these criteria: consistent API interface. To detect if two polygons are intersecting, we use the Separating Axis Theorem. There are many javascript collision routines and libraries for 2d. The technique can be used to detect collisions between sprites as an alternative to pixel-perfect collisions which are usually too slow. In any case, it should be possible to include the functions presented here to your C# projects quite straightforwardly.
So here, I'll try to keep it as simple as possible. The source codes I could find also had too many abbreviations that I don't get, or were crippled with C optimizations. It's not the first tutorial on the topic, however, the tutorials on the net tend to be a bit too complex for a relatively simple problem.
Vector 2d collision how to#
This article describes how to detect the collision between two moving (2D) polygons.


 0 kommentar(er)
0 kommentar(er)
